Niederreiter cryptosystem

In cryptography, the Niederreiter cryptosystem is a variation of the McEliece Cryptosystem developed in 1986 by Harald Niederreiter [1]. It applies the same idea to the parity check matrix H of a linear code. Niederreiter is equivalent to McEliece from a security point of view. It uses a syndrome as ciphertext and the message is an error pattern. The encryption of Niederreiter is about ten times faster than the encryption of McEliece. Niederreiter can be used to construct a digital signature scheme.

Contents

Scheme definition

Niederreiter's original proposal was broken[2] but the system is secure when used with a binary Goppa code.

Key generation

  1. Alice selects a binary (n, k)-linear Goppa code G capable of correcting t errors. This code possesses an efficient decoding algorithm.
  2. Alice generates a (n − k) × n parity check matrix H for the code G.
  3. Alice selects a random (n − k) × (n − k) binary non-singular matrix S.
  4. Alice selects a random n × n permutation matrix P.
  5. Alice computes the (n − k) × n matrix Hpub = SHP.
  6. Alice’s public key is (Hpub, t); her private key is (S, H, P).

Message encryption

Suppose Bob wishes to send a message m to Alice whose public key is (Hpub, t):

  1. Bob encodes the message m as a binary string of length n and weight t.
  2. Bob computes the ciphertext as c = HpubmT.

Message decryption

Upon receipt of c = HpubmT from Bob, Alice does the following to retrieve the message m.

  1. Alice computes S−1c = HPmT.
  2. Alice applies a syndrome decoding algorithm for G to recover PmT.
  3. Alice computes the message m via mT = P−1PmT.

Recommended values for these parameters are n = 1024, t = 38, k = 644.

Signature scheme

Courtois, Finiasz and Sendrier showed how the Niederreiter cryptosystem can be used to derive a signature scheme [3].

  1. Hash the document d to be signed (with a public hash algorithm).
  2. Decrypt this hash value as if it were an instance of ciphertext.
  3. Append the decrypted message to the document as a signature.

Verification then applies the public encryption function to the signature and checks whether or not this equals the hash value of the document. When using Niederreiter, or in fact any cryptosystem based on error correcting codes, the second step in the signature scheme almost always fails. This is because a random syndrome usually corresponds to an error pattern of weight greater than t. The system then specifies a deterministic way of tweaking d until one is found which can be decrypted.

The choice of the code parameters is related to the probability that a random syndrome is decodable. Courtois, Finiaz, and Sendrier suggest the parameter values n = 216 and t = 9. Then the probability to decode a random syndrome is 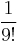\frac{1}{9!}. Therefore a decodable syndrome is found after an expected number of 9! attempts. Add a counter i to the original document d, to produce a slightly altered document di. Hashing di gives a syndrome that depends on i. Let i run from 0 to i0, with i0 the first value of i for which di is decodable. In this case the decrypted message is a word z of length n and weight 9, such that HzT equals the hash value of di0. The signature will be z combined with the value i0 for verification. This signature is attached to the original document d.

References

  1. ^ H. Niederreiter (1986). "Knapsack-type cryptosystems and algebraic coding theory". Problems of Control and Information Theory. Problemy Upravlenija i Teorii Informacii 15: 159–166. 
  2. ^ V. M. Sidel'nikov and S. O. Shestakov (1992). "On the insecurity of cryptosystems based on generalized Reed-Solomon codes". Discrete Mathematics and Applications 2 (4): 439–444. doi:10.1515/dma.1992.2.4.439. 
  3. ^ N. Courtois, M. Finiaz, N. Sendrier (2001). "How to achieve a McEliece-based Digital Signature Scheme". Advances in cryptology—ASIACRYPT 2001 LNCS 2248: 157–174. 

External links

 
Algorithms
Theory
Standardization

ANS X9F1 · CRYPTREC · IEEE P1363 · NESSIE · NSA Suite B
Topics